 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
p r e v |
Unpublished Research Outlier Detection Using Parzen
Window
This was a final semester project during my final educational degree
stint as a student in India. The goal was to detect outliers for very
high dimensional data statistically using dimensionality reduction. For
example if the data were to be obtained from a few classes, could we
devise a very fast method for such data?
|
|
It then gradually merges to the least number of clusters, c,
using a fuzzy similarity function, that minimize the sum of squared
distances of the data points to their respective cluster centers. The
cluster merging was based on thresholding the similarity at a
predetermined value much like hierarchical clustering.
Minimizing the within-cluster sum of squares of the data points does not always yield correct clusters using metrics like euclidean distances e.g. Mahalanobis distance e.g., this algorithm partitions a concentric ring data set (a main data set following a uniform circular distribution flanked by outlying data points generated from another uniform circular distribution) by a linear hyperplane. The output from the Matlab implementation of the algorithm is saved as an avi file.  |
n e x t | |||||||||||||||||||||||||||||||||||||||||||||||||
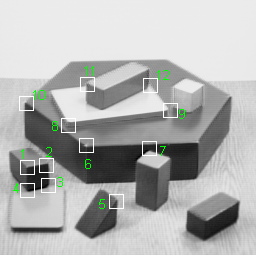
| Fig 2: DIET corner detection - Corner detection using information theory | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The middle one shows an example of the
non-parameteric density estimation of the Mahalanobis distances from
the median of the weighted data, the weights being the Tuckey's
bi-weights. The third figure on the right shows a subset of the data at
the tail of the density curve. The full report titled "Statistical Outlier Detection in Large Multivariate Datasets" can be found here Corner Detection in grayscale images using information theory Another experimentation where we were tinkering with corner detection in gray scale images using Shannon's entropy. |
The figure below only shows "some" detected
corners and their corresponding zoomed-in image regions. See Figure 2
and the
corresponding paper. Outlier Detection using Fuzzy Clustering Given a training
data set comprising of p-featured overlapping and outlying data points,
how can the outlying samples be identified while simultaneous
clustering of the data using soft computing methods. The algorithm will
run offline to obtain the value of the cut-off distance for online
identification of outlying sample points.
We implemented an algorithm using fuzzy c-means that starts clustering with an arbitrary but given number of clusters, C. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||